Filter topology
The main inspiration is from the yusynth fixed filter bank, which is actually a good starting point for a vocoder! The vocoder has a bit more band pass filters, so some calculations have to be made differently. For the band pass filters, the Q is only dependent on the values of R, so the easiest way to get the same Q for all band pass filters, is to use the same resistor values and only change the values for C.
We need two band pass filters in series to get the required -24db slope, and to get a wider “band”: so we have two band pass filters with frequencies that are to the left and the right of the actual required frequency band.
For the low- and high- pass filters, we also need a two step filter, to get the required -24db. The topologies below are only for one step each!
(to find out: multiple feedback low- & high-pass filters vs Sallen-Key low- & high-pass filters).
filters
Low pass
A Sallen-Key low-pass filter:
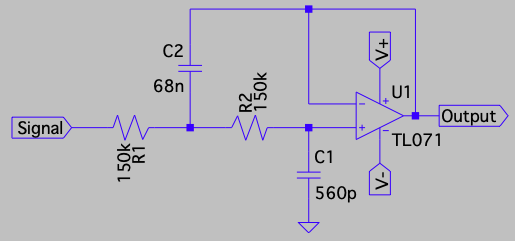
This topology uses a TL071 op amp, with a ±12V power supply and:
- \(R_1\): 150k
- \(R_2\): 150k
- \(C_1\): 560p
- \(C_2\): 68n
\[F_c = \dfrac{1}{2π\sqrt{R_1C_1R_2C_2}}, Q = \dfrac{1}{2}\sqrt{\dfrac{C_2}{C_1}}\] (NB: the \(Q\)-formula is only correct for \(R_1\) = \(R_2\)!)
- \(Q\): 5.51
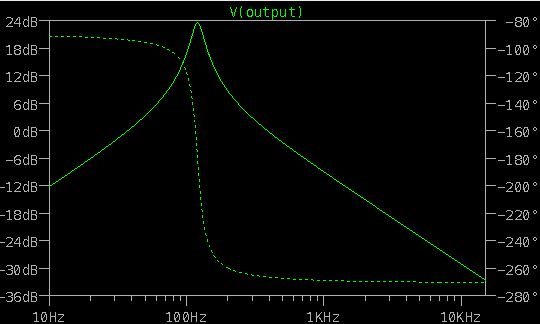
- \(F_c\): 171.9
Using ltspice, we can calculate the frequency response for this low pass filter (see lowpass.asc for the script):
High pass
A Sallen-Key high-pass filter:
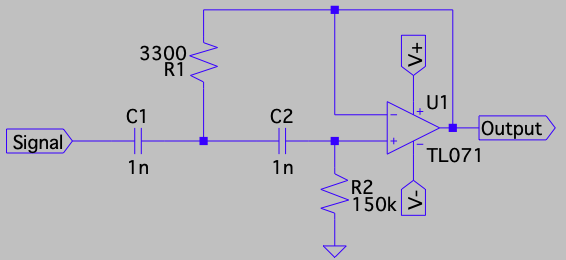
This topology uses a TL071 op amp, with a ±12V power supply and:
- \(R_1\): 3300
- \(R_2\): 150k
- \(C_1\): 1n
- \(C_2\): 1n
\[F_c = \dfrac{1}{2π\sqrt{R_1C_1R_2C_2}}, Q = \dfrac{1}{2}\sqrt{\dfrac{R_2}{R_1}}\] (NB: the Q-formula is only correct for \(C_1\) = \(C_2\)!)
- \(Q\): 3.37
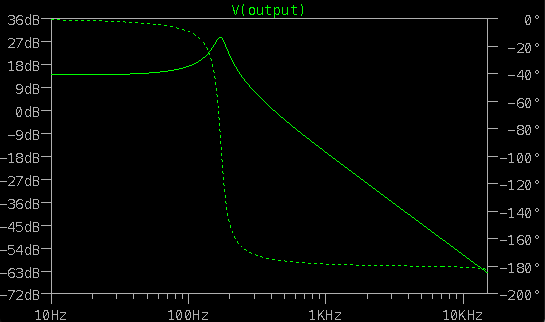
- \(F_c\): 7153.5
Using ltspice, we can calculate the frequency response for this high pass filter (see highpass.asc for the script):
Band pass
A multiple feedback band pass filter:
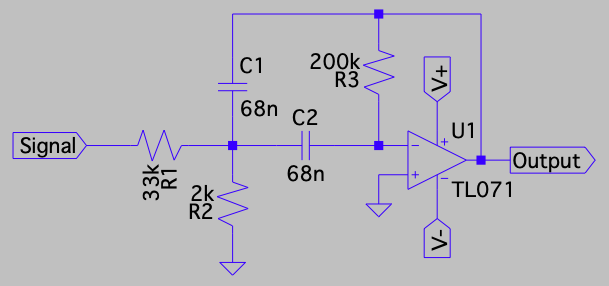
This topology uses a TL071 op amp, with a ±12V power supply and:
- \(R_1\): 33k
- \(R_2\): 2k
- \(R_3\): 200k
- \(C_1\): 68n
- \(C_2\): 68n
\[F_c = \dfrac{1}{2π\sqrt{C_1C_2R_3(\dfrac{R_1R_2}{R_1+R_2})}}, Q = \dfrac{R_3}{2\sqrt{R_3(\dfrac{R_1R_2}{R_1+R_2})}}\] (NB: the Q-formula is only correct for \(C_1\) = \(C_2\)!)
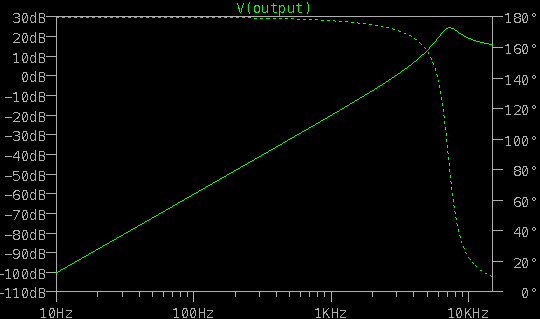
- \(Q\): 5.15
- \(F_c\): 120.5
Using ltspice, we can calculate the frequency response for this band pass filter (see bandpass.asc for the script):